Geometry

Geometry (formerly Hendese) is the branch of mathematics that deals with spatial relationships. The name is derived from the Greek Γεωμετρία “Geo” (place) and “metro” (measurement).

Geometry is derived from the words land measurement. Herodotus (450 BC) accepts that the origin of geometry is Egypt. According to him, the concept of geometry is of Egyptian origin. The use of the word goes back to Plato, Aristotle and Thales. However, Euclid preferred the word Elements instead of the word geometry. The Greek equivalent of the word Elements is the word stoicheia.

A suitable structure placed on a set and relating the elements of the set to each other makes it possible to do geometry. The name of the “high school geometry” that will be naturally placed on a plane and will take into account the intuitive sense of distance is Euclidean geometry. A historically interesting and important feature of this geometry is the parallelism axiom. Geometries that do not satisfy this axiom but satisfy all the other axioms are called non-Euclidean geometries. Hyperbolic geometry or spherical geometry can be given as examples of these. There is also non-measurement geometry, which is worked on using nothing but a ruler, triangle and compass without scale.

Plane Geometry ( 2-D Geometry)

Plane geometry is concerned with the shapes that can be drawn on paper. Euclidean geometry involves the study of plane geometry.

A 2D surface spread infinitely in both directions is referred to as a plane. The basic components of the plane are:

• Points – A point is the no-dimensional fundamental unit of geometry.
• Lines – A line is a straight path on a plane that extends in both directions with no endpoints.
• Angles – Plane geometry consists of lines, circles, and triangles of two dimensions. Plane geometry is another name for two-dimensional geometry.

Important Points in Plane Geometry

• Collinear points are the ones that lie on the same line.
• A line segment is part of a line that has two endpoints and is finite in length.
• A ray is a line segment that extends indefinitely in one direction. A line has no endpoints.
• Line, line segment, and ray are different from each other.

All two-dimensional figures have only two dimensions: length and width. Plane figures consist of squares, triangles, rectangles, circles, and so on.

Angles in Geometry

In planar geometry, an angle is formed when two rays intersect, called the sides of the angle, and share a common endpoint known as the vertex of the angle.

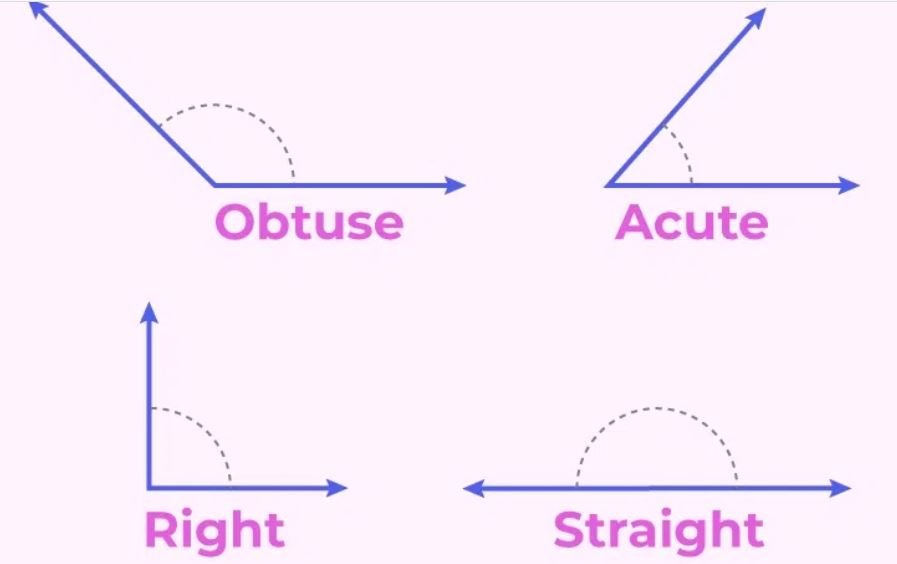
There are majorly four types of angles

1. Acute Angle–  An Angle between 0 to 90°.
2. Obtuse Angle– An angle more than 90° but less than 180°.
3. Right Angle– An angle of 90°.
4. Straight Angle– An angle of 180° is a straight line.

Polygon

A figure that is made up of a finite number of straight-line segments closing in a loop. The word ‘poly’ means multiple.

The sum of internal angles of a polygon is : (n-2) * 180 

where n is the number of sides.

Types of Polygon

The types of polygons are:

Name	Number of Sides	Number of vertices	Number of diagonals	Interior Angle Measure for Regular Polygon
Triangle	Polygons with 3 sides	3	0	60°
Quadrilateral	Polygons with 4 sides	4	2	90°
Pentagon	Polygons with 5 sides	5	5	108°
Hexagon	Polygons with 6 sides	6	9	120°
Heptagon	Polygons with 7 sides	7	14	128.571°
Octagon	Polygons with 8 sides	8	20	135°
Nonagon	Polygons with 9 sides	9	27	140°
Decagon	Polygons with 10 sides	10	35	144°

Geometry is one of the oldest branches of mathematics that is concerned with the shape, size, angles, and dimensions of objects in our day-to-day life. Geometry in

Circle in Geometry

A circle is a closed shape. From a fixed point known as the center, all the points of a circle are of the same distance.

Similarity and Congruency in Geometry

Similarity: Two figures are considered similar if they have the same shape or equal angle but may not be necessarily of the same size.

Congruence: Two figures are said to be congruent if they are the same shape and size i.e. they are equal in all means.

Solid geometry is the study of three-dimensional structures such as cubes, prisms, cylinders, and spheres. 3D figures’ three dimensions are length, width, and height. However, certain solids do not have faces (e.g. sphere).

The analysis of three dimensions in Euclidean space is known as solid geometry. The structures of our environment are three-dimensional.

Both three-dimensional shapes are created by rotating two-dimensional shapes. Essential characteristics of 3D forms are :

• Faces
• Edges
• Vertices

Edges

An edge is the line segment that joins one vertex to another. It helps in forming the outline of 3D shapes. It means it joins one corner point to another.

Faces

It is defined as the flat surface enclosed by edges that geometric shapes are made up of. It is a 2D figure for all 3D figures.

Vertices

A vertex is a point where the edges of the solid figure meet each other. It can be referred to as a point where the adjacent sides of a polygon meet. The vertex is the corner where edges meet.

The number of edges, faces and vertices in different solid shapes is given in the table:

Solid Shapes	No. of. Edges	No. of. Faces	No. of. Vertices
Triangular Prism	9	5	6
Cube	12	6	8
Rectangular Prism	12	6	8
Pentagonal Prism	15	7	10
Hexagonal Prism	18	8	12
Triangular Pyramid	6	4	4
Square Pyramid	8	5	5
Pentagonal Pyramid	10	6	6
Hexagonal Pyramid	12	7	7

Geometry

Three-dimensional geometry studies the geometry of shapes in 3D space in the cartesian planes. Every point in the space is referred by 3 coordinates, (x, y, z) that are real numbers.

Geometry Formulas

This are some fundamental geometry formulas:

1. Area Formulas

•     Rectangle: Area = length × width
•     Square: Area = side × side (or side²)
•     Triangle: Area = ½ × base × height
•     Circle: Area = π × radius²

2. Perimeter/Circumference Formulas

•     Rectangle: Perimeter = 2 × (length + width)
•     Square: Perimeter = 4 × side
•     Triangle: Perimeter = side₁ + side₂ + side₃
•     Circle: Circumference = 2 × π × radius

3. Volume Formulas

•     Cube: Volume = side × side × side (or side³)
•     Rectangular Prism: Volume = length × width × height
•     Cylinder: Volume = π × radius² × height
•     Sphere: Volume = ⁴⁄₃ × π × radius³

4. Pythagorean Theorem

    For a right triangle with sides , , and hypotenuse : .

5. Trigonometric Ratios (for right triangles):

•     Sine (sin): sin(θ) = opposite / hypotenuse
•     Cosine (cos): cos(θ) = adjacent / hypotenuse
•     Tangent (tan): tan(θ) = opposite / adjacent

These are just a few basic formulas; geometry encompasses a wide range of concepts, each with its own set of formulas and principles.

Application of Geometry in Real Life

• Imagine standing before a towering skyscraper or walking through a charming bridge. The awe-inspiring shapes and the strength of these structures owe much to geometry, guiding architects and engineers in creating spaces that are not only safe but also pleasing to the eye.
• Art and design are playgrounds for geometric exploration. Artists manipulate shapes and forms to produce stunning visuals, while designers use geometry to bring balance and harmony to everything from sleek websites to cozy living rooms.
• Next time you lose yourself in a video game or a movie’s CGI wonders, remember that geometry is the secret spell behind those captivating visuals. It helps animate characters and build fantastical worlds that seem nearly as tangible as our own.
• The art of cartography, or map-making, transforms the round globe into a flat map with the help of geometry, helping us navigate from point A to point B, whether it’s through bustling city streets or across continents.
• The vastness of space becomes a little more understandable with geometry. It calculates distances to far-off stars and plots the courses of space missions, turning the mysteries of the universe into solvable puzzles.
• In the realm of medicine, geometry’s precise calculations are crucial for technologies like CT scans and MRIs, offering doctors a glimpse inside the human body to diagnose and treat illnesses with remarkable accuracy.
• The convenience of GPS technology, guiding you on your travels or ensuring your online orders arrive at your doorstep, is powered by geometric principles, ensuring accuracy and efficiency in navigation.
• From assembly lines to household helpers, robots rely on geometry to move gracefully and interact with their surroundings, making them indispensable tools in modern manufacturing and daily convenience.
• The next time you dress up or admire a piece of jewelry, consider the geometric principles that influence fashion design, from the symmetry of patterns to the structure of garments.
• Sports aren’t just about physical prowess; they’re also about strategy. Athletes and coaches use geometry to plot game-winning moves, whether it’s the perfect soccer goal or the ideal swim turn.

Geometry Solved Examples

Example 1: If the equal angles measure 50° in an Isosceles triangle then find the third angle.

Solution:

Let the third angle be x

We know that sum of the three angles of a triangle is 180

⇒ x + 50° + 50° = 180°

⇒ x + 100° = 180°

⇒ x = 180° – 100° = 80°

Hence, the third angle measure 80°

Example 2: If one of the angle measure 70° in a parallelogram, find the rest of all the angles.

Solution:

We know that the sum of the adjacent angles of a parallelogram is 180°. Let the angle adjacent to 70° be x

⇒ 70° + x = 180°

⇒ x = 180° – 70° = 110°

We also know that opposite angles of a parallelogram are equal. Hence, the angle opposite 70° will be 70° and the angle opposite 110° will be 110°

Example 3: If a line of length 3 cm is perpendicular to the Chord of the circle 8 cm then find the radius of the circle.

Solution:

We know that a perpendicular from the center to the chord bisects the chord. Hence, the line from the center will touch the midpoint of the chord such that the length of the line on either side measures 4 cm. Now the perpendicular from the center, half of the chord, and the radius will form a right-angled triangle where the radius will be the hypotenuse of the triangle. Hence, the radius of the circle will be given by using the Pythagoras theorem,

r = √3² + 4² = √25 = 5 cm

Example 4: Find the area of the triangle whose base is 24 cm and height is 12 cm.

Solution:

Area of a triangle is given by 1/2 ⨯ base ⨯ height

Here, base = 24 cm, height = 12 cm

Hence, Area of the triangle is 1/2 ⨯ 24 ⨯ 12 = 144cm²

Example 5: Find the area and circumference of a circle whose radius is 7cm.

Solution:

Given that radius = 7 cm

Circumference of a Circle = 2πr = 2 ⨯ 22/7 ⨯ 7 = 44 cm

Area of Circle = πr² = 22/7 ⨯ 7 ⨯ 7 = 154 cm²