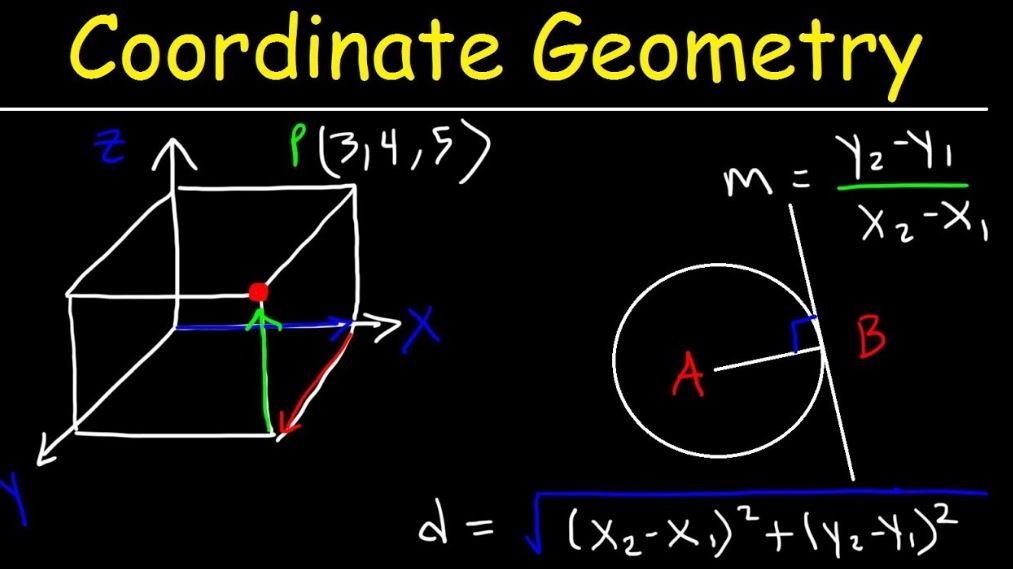
In our previous article, we provided detailed information about geometry and shared basic geometry formulas with you. In this article, we cover the topic of Coordinate Geometry.
Coordinate geometry is a branch of mathematics that deals with plotting curves on coordinate axes. Various curves can be plotted on the coordinate plane using coordinate geometry formulas. Coordinate geometry uses algebraic equations to plot various curves on the coordinate plane.
What is Coordinate Geometry?
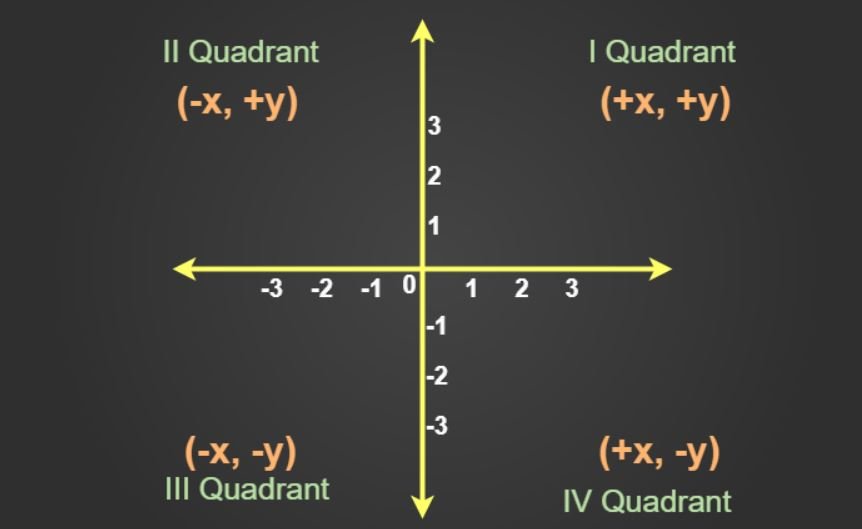
Coordinate geometry is a branch of mathematics, which is used to represent various geometric figures in a 2-D plane. Coordinate geometry is used to describe various curves such as circles, parabolas, etc. Coordinate geometry divides the coordinate plane into four different quadrants, which are the I quadrant, II quadrant, III quadrant, and IV quadrants.
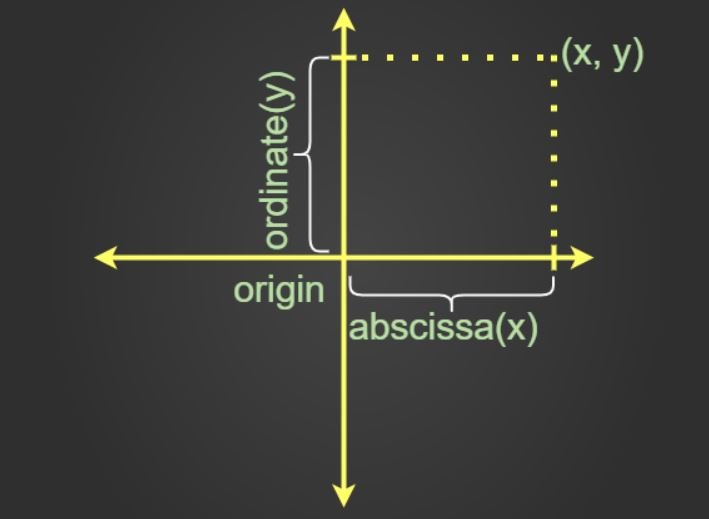
A coordinate is an address, which helps to locate a point in space. For a two-dimensional space, the coordinates of a point are (x, y). Here let us take note of these two important terms.
- Abscissa: It is the x value in the point (x, y), and is the distance of this point along the x-axis, from the origin.
- Ordinate: It is the y value in the point (x, y)., and is the perpendicular distance of the point from the x-axis, which is parallel to the y-axis.
The coordinates of a point are useful to perform numerous operations of finding distance, midpoint, the slope of a line, and equation of a line.
The coordinates of a point are the real variables associated in an order to describe its location in space. Here we consider the space to be two-dimensional. Let’s have a look at the following terms.
- Origin: Through a point O, referred to as the origin, we take two mutually perpendicular lines XOX’ and YOY’, and call them x and y axes respectively.
- Abscissa & Ordinate: The position of a point is completely determined with reference to these axes by means of an ordered pair of real numbers (x, y) called the coordinates of P where | x | and | y | are the distances of the point P from the y-axis and the x-axis respectively, x is called the x-coordinate or the abscissa of P and y is called the y-coordinate or the ordinate of the point P.
Coordinate Geometry Formulas
The formulas of coordinate geometry help in conveniently proving the various properties of lines and figures represented in the coordinate axes. The formulas of coordinate geometry are
- Distance Formula
- Mid-Point Formula
- Section Formula
- Slope Formula
- Area of Triangle
Let us know more about each of the formulas in the below paragraphs.
Distance Formula
The distance between two points A(x1, y1) and B(x2, y2) is given by
AB = √((x2 – x1)2 + (y2 – y1)2)
The distance of the point P(x, y) from the origin O(0, 0) is given
OP = √((x – 0)2+ (y – 0)2), i.e. OP = √(x² + y²)
Example: Find the distance between the points P(-4, 7) and Q(2, -5).
Solution:
The given points are P(-4, 7) and Q(2, -5).
Then, (x1 = -4, y1 = 7) and (x2 = 2, y2 = -5). :
PQ = √((x2 – x1)2 + (y2 – y1)2)
= √((2 – (-4))2 + (-5 – 7)2)
= √(62 + (-12)2)
= √(36 + 144)
= √180
= 6√5
Mid-Point Formula
The midpoint is the point that divides any line segment into two equal parts. The formula to find the midpoint of the line with endpoints A(x1, y1) and B(x2, y2) is given by,
midpoint (x,y) = {(x1+x2)/2 , (y1+y2)/2}
Example: Find the coordinates of the midpoint of the line segment joining points A(-5, 4) and B(7,-8).
Solution:
Let M(x, y) be the midpoint of AB. Then,
x = ((-5) + 7)/2 =1 and y = ((4 + (-8)) = -2
Hence, the required point is M (1, -2).
Section Formula
The coordinates of the point P(x, y) which divides the line segment joining A(x1, y1) and B(x2, y2) internally in the ratio m:n are given by
x = (mx2 + nx1) / (m+n)
y = (my2+ny1) / (m+n)
Example: Find the coordinates of the point that divides the line segment joining the points A(5, 4) and B(7,8) in the ratio of 2:3.
Solution:
Let M(x, y) be the required point,
given m:n = 2:3 and (x1, y1) = (5, 4) , (x2, y2) = (7,8)
now for M(x,y)
x = (mx2 + nx1) / (m+n)
= (2×7 + 3×5)/(2 + 3)
= 29/5
y = (my2+ny1) / (m+n)
= (2×8 + 3×4)/(2 + 3)
= 40/5
= 8
So, the required point M(x,y) is (29/5 , 8)
Slope Formula
The slope of a line is the inclination of the line. Slope Formula is calculated by measuring the angle made by the line with the positive x-axis, or by calculating it using any two points on the line. The slope of a line inclined at an angle θ with the positive x-axis is given by m = tan θ. The slope of a line joining the two points A(x1, y1) and B(x2, y2) is given by
m = tan θ = (y2-y1) / (x2-x1)
Example: Find the slope of the line segment joining by points A(5, 1) and B(7,8).
Solution:
given, (x1, y1) = (5, 1) , (x2, y2) = (7, 8)
Slope (m) = (y2-y1) / (x2-x1)
= (8-1)/(7-5)
= 7/2
Area of Triangle
The area of a triangle ABC with vertices A(x1, y1), B(x2, y2), and C(x3, y3) is given by
area(ABC) = |1/2 {x1(y2 – y3) + x2(y3 – y1) + x3 (y1 – y2)}|
Example: Find the area of the triangle whose vertices are A(2, 7), B(3, -1), and C(-5, 6).
Solution:
Let A(2, 7), B(3, -1) and C(-5, 6) be the vertices of the given △ABC.
Then,
(x1 = 2, y1 = 7), (x2 = 3, y2 = -1) and (x3 = -5, y3 = 6).
Area of △ABC = |1/2 {x1(y2 – y3) + x2(y3 – y1) + x3 (y1 – y2)}|
= 1/2 |2(-1 – 6) + 3(6 – 7) – 5(7 +1)|
= 1/2| -14 – 3 – 40|
= 1/2|-57|
= 57/2
= 28.5 sq units.
Read More about Area of Triangle.
Condition for Collinearity of Three Points
Let the given points be A(x1, y1), B(x2, y2), and C(x3, y3). Then A, B, and C are collinear,
area of ABC = 0
1/2[x1(y2 – y1) + x2(y3 – y1) + x3(y1 – y2)] = 0
Example: Show that points A(-1, 1), B(5, 7), and C(8,10) are collinear.
Solution:
Let A(-1, 1), B(5, 7) and C(8, 10) be the given points.
Then, (x1 = -1, y1 = 1), (x2 = 5, y2 = 7) and (x3 = 8, y3 = 10)
∴ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)
= (-1) (7 – 10) + 5(10 -1) + 8(1 – 7)
= (3 + 45 – 48)
= 0
Hence, the given points are collinear.
Centroid of a Triangle
Centroid of a triangle is the point of intersection of all three medians of a triangle. The centroid of a triangle having its vertices A(x1,y1), B(x2,y2), and C(x3,y3) is given by the formula
Centroid (x,y) = {(x1+x2+x3) / 3, (y1+y2+y3) / 3}
Example: Find the centroid of the triangle whose vertices are A(2, 7), B(3, -1), and C(-5, 6).
Solution:
Let A(2, 7), B(3, -1) and C(-5, 6) be the vertices of the given △ABC.
(x1 = 2, y1 = 7), (x2 = 3, y2 = -1) and (x3 = -5, y3 = 6).
Centroid (x,y) = {(x1+x2+x3) / 3 , (y1+y2+y3) / 3}
= {2+3+(-5)}/3 , {7+(-1)+6}/3
= (0 , 12)
Solved Examples on Coordinate Geometry
Example 1: Show that the points A(a, b + c), B(b, c + a), and C(c, a + b) are collinear.
Solution:
Let A(a, b + c), B(b, c + a) and C(c, a + b) be the given points. 11
Then, (x1 = a, y1 = b + c); (x2 = b, y2 = c + a); and (x3 = c, y3 = a + b).
∴ a(c + a – a – b) + b(a + b – b – c) + c(b + c – c – a)
= a(c – b) + b(a – c)+ c(b – a)
= 0
Hence, the given points are collinear.
Example 2: Find the area of quadrilateral ABCD whose vertices are A(-4, -2), B(-3, -5), C(3, -2), and D(2, 3).
Solution:
Join A and C. Then, area of quad. ABCD = ar(△ABC) + ar(△ACD)
Area of △ABC = 1/2|{(-4).(-5 + 2) -3(-2 + 2) + 3(-2 + 5)}|
= 21/2 sq units.
Area of △ACD = 1/2|{ (-4).(-2 – 3) + 3(3 + 2) + 2(-2 + 2}|
= 35/2
Area of quad. ABCD = 21/2 + 35/2 sq units = 28 sq units.
Example 3: Find the coordinates of the points of trisection of the line segment joining the points A(-5, 6) and B(4, -3).
Solution:
Let P and Q be the points of trisection of AB.
Then, P divides AB in the ratio 1 : 2
So, the coordinates of P are
P((1 x 4 + 2 x (-5)/1 + 2, ((1 x (-3) + 2 x 6)/1 + 2) i.e., P(-2, 3).
Also, Q divides AB in the ratio 2:1.
So, the coordinates of Q are
Q((2 x 4 + 1 x (-5)/2 + 1, (2x(-3) +1 x 6/1 + 2)) i.e., Q(1, 0)
Q(1, 0).
Example 4: Find the distance of point P(6, -6) from the origin.
Solution:
Let P(6, -6) be the given point and O(0, 0) be the origin.
Then, OP = √((6 – 0)2 + (-6 – 0)2)
= √(62 + (-6)2)
= √72
= 6√2