Polynomial Formula gives the standard form of polynomial expressions. It specifies the arrangement of algebraic expressions according to their increasing or decreasing power of variables.
What is Polynomial?
Algebraic expressions with non-negative power are called polynomials. Polynomials are the addition of monomials, binomials, and others.
The degree of a polynomial can be calculated by finding the highest power of the variable in the given polynomial.
For example, f(x) = 3x2 + 4x + 5 is a polynomial with a degree of 2. The polynomial formula has both like terms and unlike terms.
- Like terms have the same powers of the same variable.
- Unlike terms have different variables and different powers.
Types of Polynomial
Different Types of Polynomial have been discussed in the table below :
| Type of Polynomial | Description | General Formula | Example |
|---|---|---|---|
| Monomial | Polynomials with one term | axn | x, y², 3y³, etc. |
| Binomial | Polynomials with two terms | axn+ bym | 2x + y², x + 3y³, etc. |
| Trinomial | Polynomials with three terms | axn + bym + czk | 2x + z + y², z – x + 3y³, etc. |
| Quadratic Polynomial | Second-degree polynomial (typically two or three terms) | ax2+ bx + c | 2x + y² + 3y³, etc. |
What is Polynomial Formula?
The standard form of a polynomia is called the polynomial formula. It consists of a combination of algebraic expressions arranging in ascending/descending order of powers.
Polynomial Formula
The General Formula of Polynomial is :
axn + bxn-1 + cxn-2 +…+ px + q
Where,
- a, b, c, …, p and q are coefficients,
- x is the variable,
- n is the degree of the polynomial.
The above formula can be easily arranged in the following manner:
f(x) = an(xn)
Where,
- a is the coefficient,
- x is the variable,
- n is the exponent.
Some other important polynomial formula are :
- f(x) = anxn + an-1xn-1 + an-2xn-2 + … + a1x +a0
- f(x) = anxn + … + px + q
Quadratic Equation Formula
The standard form of Quadratic Equation is given by :
ax2+ bx + c = 0
Cubic Equation Formula
The standard form of Cubic Equation is given by :
ax3 + bx2+ cx + d = 0
Polynomial Identities
Let’s learn some of the algebraic identities of polynomials and their expansion.
| Identity | Expansion |
|---|---|
| (x + y)² | x² + 2xy + y² |
| (x – y)² | x² – 2xy + y² |
| x² – y² | (x + y)(x – y) |
| (x + y)³ | x³ + y³ + 3xy(x + y) |
| (x – y)³ | x³ – y³ – 3xy(x – y) |
| x³ + y³ | (x + y)(x² – xy + y²) |
| x³ – y³ | (x – y)(x² + xy + y²) |
| x³ + y³ + z³ – 3xyz | (x + y + z)(x² + y² + z² – xy – yz – zx) |
| (x + a)(x + b) | x² + (a + b)x + ab |
| (x + y + z)² | x² + y² + z² + 2xy + 2yz + 2zx |
Applications of Polynomial Formula
Polynomial Formula has the following applications :
- They are used to define the equation of various forces, paths, and other concepts in detail.
- Polynomial equations are used to explain unknown quantities and their relation with other quantities in detail.
- Polynomial formulas are used to solve various complex mathematical equations.
- They are used to estimate the curves of the roller-coaster tracks to estimate the suitable curvature and height of the tracks.
- They are used to correctly estimate the stock markets and accordingly shares can be purchased or sold.
Solved Examples on Polynomial Formula
Example 1: Find the factors of the given polynomial x2 + 5x + 6
Solution:
Given polynomial,
x2 + 5x + 6
= x2 + 2x + 3x + 6
= x(x + 2) + 3(x + 2)
= (x + 2)(x + 3)
So factors of given polynomial are (x + 2) and (x + 3)
Example 2: Find the factors of the given polynomial x2 + 3x – 4
Solution:
Given polynomial,
x2 + 3x – 4
= x2 + 4x – x – 4
= x(x + 4) – 1(x + 4)
= (x + 4)(x – 1)
So factors of given polynomial are (x + 4) and (x – 1)
Example 3: Find the factors of the given polynomial x2 – 7x + 12
Solution:
Given polynomial,
x2 – 7x + 12
⇒ x2 – 4x – 3x + 12
⇒ x(x – 4) – 3(x – 4)
⇒ (x – 4)(x – 3)
So factors of given polynomial are (x – 4) and (x – 3)
Example 4: Simplify (x2 + 6x + 9) / (x + 3)3
Solution:
Given, (x2 + 6x + 9) / (x + 3)3
Now simplifying,
x2 + 6x + 9
= x2 + 3x + 3x + 9
= x(x + 3) + 3(x + 3)
= (x + 3)(x + 3)
= (x + 3)2
(x2 + 6x + 9) / (x + 3)3 = (x + 3)2 / (x + 3)3
= 1/(x+3)
Example 5: Expand (3x – 11)3 using the cubic polynomial formula.
Solution:
We know that, (x – y)3= x3 – y3 – 3xy (x – y)
Now, (3x – 11)3
= (3x)3 – (11)3 – 3(3x)(11)(3x-11)
= 27x3 – 1331 – 9x(3x -11)
This is the required expansion.
Example 6: Divide the polynomial x3 – 6x2 +3x + 10 by x + 1
Solution:
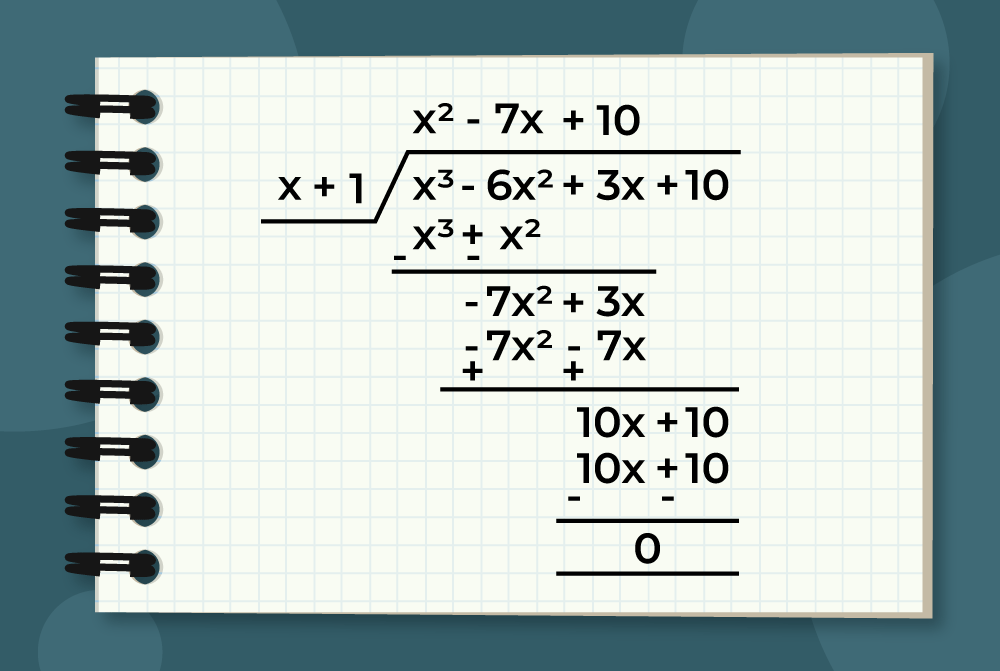
Practice Problems
Problem 1: Evaluate the polynomial at given values: P(x) = 3x4 − 5x3 + 2x2 − x + 7
- P(1)
- P(−2)
- P(0)
Problem 2: Factor the polynomial completely: x3 − 6x2 + 11x − 6
Problem 3: Find the roots of the polynomial: 2x2 − 4x − 6 = 0
Problem 4: Simplify the polynomial expression: (3x2 + 2x − 5) + (2x2 − 3x + 4)
Problem 5: Multiply the polynomials: (2x − 3)(x2 + x + 4)
Polynomial Formulas- FAQs
What is the Polynomial Formula in Algebra?
Polynomial Formula consists of the different combinations of algebric expressions arranged in the ascending/descending forms. A standard form of the polynomial formula can be given as,
axn + bxn-1 + cxn-2 +…..+ px + q
What is n in Polynomial Formula?
For any polynomial, the power of the highest term is called as the degree of the polynomial. It is denoted as n.
What is the formula of Quadratic Polynomial?
A polynomial with degree 2 is called a quadratic polynomial. The polynomial formula for Quadratic Polynomials is,
ax2 + bx + c
Where a, b and c are the real numbers.
What is the polynomial formula cubed ?
The cubed polynomial formula is, (x+y)3 = x3 + y3 + 3xy (x + y)
What is the degree of polynomial?
The term with the highest power in any polynomial formula is called the degree of the polynomial.




