Fractions are numerical expressions used to represent parts of a whole or ratios between quantities. They consist of two numbers separated by a horizontal line called a vinculum, where the number above the line is called the ‘Numerator’ and the number below the line is called the ‘Denominator’.
Example, If A pizza is divided into 4 equal parts, and one part is taken out, thus the fraction representing the taken out part is 1/4 as one part is taken out of 4 equal parts.
If 3 parts are taken then the fraction representing the taken out part will be 3/4.
Parts of Fraction
If we divide anything into some equal parts then, a fraction consists of two main parts:
- Numerator : The number at the top of the fraction, representing the number of parts being considered.
- Denominator : The number at the bottom of the fraction, representing the total number of equal parts into which the whole is divided.
Use the following tools to understand the fraction:
Fractions in Real Life
Fractions are everywhere in daily life, helping us divide things into equal parts, represent ratios, and make comparisons. Some common examples are:
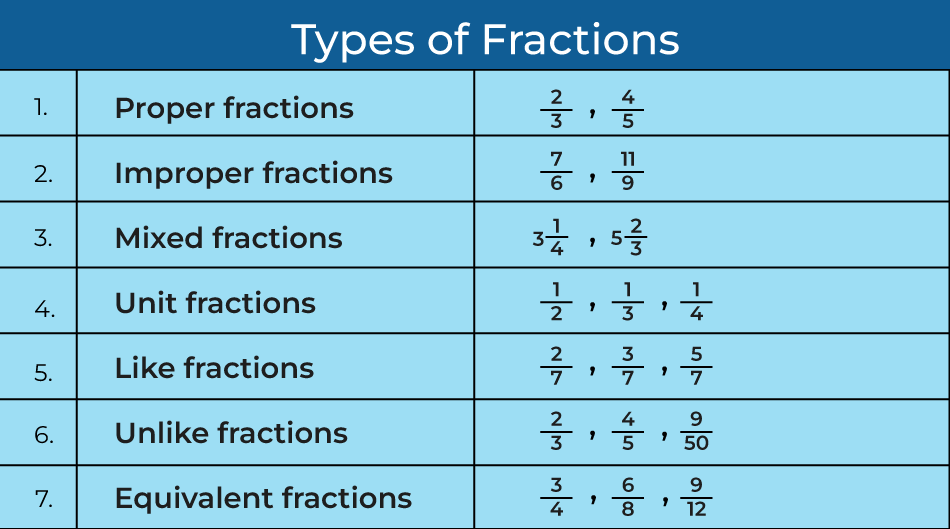
Types of Fractions
There are majorly seven types of fractions. They are unit fractions, proper fractions, improper fractions, and mixed fractions, like fractions and unlike fractions, equivalent fraction. They are categorized on the basis of their numerator and denominator.
Proper Fraction: Fractions in which the numerator value is less than the denominator value.
Improper Fractions:Fraction in which the numerator value is greater than the denominator value.
Mixed Fractions:Fraction that consists of a whole number with a proper fraction.
Like Fractions: Fractions whose denominators are the same are known as like fractions
Unlike Fractions: Fractions whose denominators are different are called, unlike fractions.
Unit Fraction: Fraction with 1 as a numerator and is known as a Unit Fraction. All unit fractions are proper fractions since all unit fractions have 1 in the numerator, which is lesser than the denominator.
Equivalent Fractions: Fractions which result in the same value after simplification.
Representing Fractions on a Number Line
Fractions on a number line are shown between two integers. The whole is divided into equal parts based on the denominator, and the numerator shows the fraction’s position.
Example, to represent 1/8, divide the space between 0 and 1 into 8 parts. The first part is 1/8, the second is 2/8, and so on.

Properties of Fractions
There are some important properties of fractions similar to whole numbers, natural numbers, etc. Let’s take a look at those properties:
| Property | Description | Example |
|---|---|---|
| Commutative Property (Addition & Multiplication) | The order of adding or multiplying fractions doesn’t change the result. |
Addition: a/b + c/d = c/d + a /b Multiplication: a/b × c/d = c/d × a /b |
| Associative Property (Addition & Multiplication) | The way fractions are grouped in addition or multiplication doesn’t change the result. |
Addition: (a/b + c/d )+ e/f = a/b + (c/d )+ e/f ) Multiplication: (a/b × c/d) × e/f = a/b × (c/d × e/f) |
| Identity Element | For multiplication, the identity is 1 (multiplying a fraction by 1 gives the same fraction). For addition, the identity element is incorrectly noted as 0 in the statement; it should be that adding 0 to a fraction doesn’t change its value. |
Multiplication: (a/b) ×1 =a/b Addition: a/b+0 =a/b |
| Multiplicative Inverse | The reciprocal of a fraction, when multiplied by the original fraction, gives 1. | (a/b) × (b/a) = 1 |
| Distributive Property | Multiplying a fraction by the sum of two fractions equals the sum of each multiplied separately. | a/b × (c/d + e/f) = a/b × c/d + a/b× e/f |
Solved Examples on Fractions
Example 1: Write two equivalent fractions of 3/39.
Solution:
Given, fraction : 3/39
Equivalent fraction by multiplying with the same number, lets multiply by 2:
= (3 × 2)/(39 × 2)
= 6/78Equivalent fraction by division with the same number, here, both numerator and denominator are divisible by 3, dividing by 3:
= (3 ÷ 3)/(39 ÷ 3)
= 1/13
Example 2: In a class of 90 students, 1/3rd of the students do not like cricket. How many students like cricket?
Solution:
Fraction of students that do not like cricket = 1/3
Fraction of student that like cricket = 1 – 1/3= (3 – 1)/3
= 2/3rd students like cricket.Number of students that like cricket = 2/3 × 90
= (2 × 30)
= 60Therefore, 60 students like cricket.
Example 3: What type of fraction is this – 1/2, 1/5, 1/7, 1/10, 1/3?
Answer:
This is a Unit fraction because all the fractions have 1 as a numerator.
Example 4: If a recipe needs 3/4 cup of sugar and you want to make twice the quantity mentioned in the recipe, how much sugar do you need?
Answer:
Sugar needed for recipe = 3/4 cup
Sugar needed for half the recipe = 2 × 3/4
Required sugar = 2× 3/4 = 6/4Therefore, we need 6/4 cup of sugar.